Session 7: Diffusion part 3, Score-based generative models

• Now change pictures; 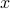represents a data point in some abstract data space now, either pixels of an image, or some representation of a protein structure.

• Review: a diffusive process can be described two ways, either as a stochastic trajectory of 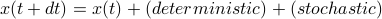– or as a diff eq of the probability density, deterministically evolving over time (which also has the corresponding force / diffusion terms).

  • Discuss the straightforward way to simulate this with Euler integration, step by step.

  • If particle starts at 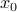at time 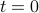and undergoes dynamics with constant drift and constant diffusion coefficient, then .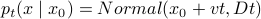

  • If instead force term is 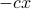(pull towards origin) then (work this out…at long times it is a zero-centered Gaussian)

  • Finally introduce the generalization of this: “variance-preserving” process from Song 2021, with time-dependent schedule at which noise is injected, 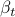. Note how the stationary distribution is indepdendent of …

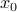• What if at 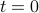, the particle were not localized at a single point 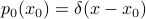, but had another arbitrary distribution? Write the convolution expression for 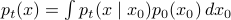and interpret this. And note that for large 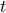, this is approximately the stationary dist.

• Claim the remarkable fact that diffusion equations can have a time-reversed partner with the same (Backward) Kolmogorov equation!

Here is where my understanding gets hazy.

• Discuss what the score means, 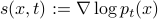, and why knowing it is useful

• Write down the objective function (score matching, appropriately weighted across 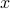and )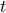

• And what the sampling process looks like (Euler integration of the reverse, denoising process, from the prior distribution.)

Leave a Comment Below!