Session 1: The Boltzmann distribution and temperature

• Intro: language of probability distributions are used to model both biomolecular systems, and data points used in machine learning. Analogies can be drawn between both, especailly when data points are literally biomolecules!

• Simple enough: let 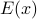be energy, then take 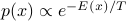. Discuss probability weights vs normalized probs

• Work through simple examples in low 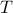/ high 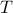limit to gain intuition:

  • two-state system (NMR, fold unfold, open close)

  • twenty-state discrete system (AA logits)

  • Quadratic potential of a 1d continuous variable (Optical trap, spring, rod bending)

    • spend some time with this as it becomes relevant later on! Note the Gaussian distribution in x, and how width depends on temperature and spring constant.

  • arbitrary 1d potential, e.g. an asymmetric double well potential

    • illustrate multiple modes and what delta E between minima tells you (or doesn't) (rxn coordinate picture in chemistry)

    • describing open/close state of a channel, along some suitable “reaction coordinate”.

    • What changes between low T and high T?

  • N-dimensional isotropic / anisotropic Gaussians, quadratic forms, covariances, etc. (Maxwell-Boltzmann, normal modes, PCA)

  • Finally, general 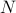-dimensional case (protein conformational dynamics, data points in ML)

• Preview up ahead:

  • Multiple modes, is there a simpler way to describe? (yes – free energy)

  • Can we think of dynamics leading to equilibrium? (Langevin dynamics) What is the probability distribution over? (time averages)

  • How is this useful for machine learning and data distributions? (Energy-based models, exponential family models)

Leave a Comment Below!