Session 2: Energy, entropy, and the free energy
Be able to explain the tradeoff between energy and entropy, its relevance for protein biophysics, and the motivation for defining the free energy as having the two terms.
Today we discuss the interpretation of entropy and free energy, from a protein biophysics point of view. Why should we care?
fundamental ‘molecular driving force’ behind protein biophysics: dynamics, multiple states, etc.
useful language for describing high dimensional probability distribution
Simpler ‘collective variables’ are necessary when describing systems with many, many variables!
e.g. a protein has thousands of atoms, so thousands of xyz coordinates are required for the full microscopic description
however, for many things you care about, it's sufficient to use a ‘collective variable’ that grossly captures the overall features. examples include
an angle of some helix
volume withinin an internal cavity
activation of a receptor
open or close state of an ion channel
end-to-end length from the carboxy to amino end of the chain
the interplay between microscopic picture and these ‘coarse-grained’ sorts of variables is at the heart of stat mech.
For simplicity, let's divide our total phase space (i.e. space of all possible microscopic configurations) into two parts, labeled A and B. How do we find the total probability of part A vs of part B?
Case 1: all microstates have the same energy, but
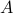has 
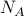states and 
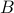has 
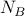states.then
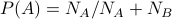, etc., just by counting number of states.
Case 2: what if all of the ‘A’ states have energy
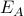and the ‘B’ states have energy 
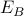?then just weight accordingly by Boltzmnn factor:
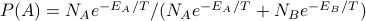
Note that this can be rewritten as
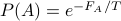where 
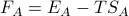and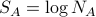 
!
Case 3: group A states have energy
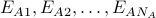and group B states have energy 
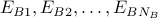.can still in general define
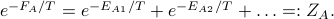
Solving for
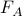we get 
.
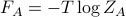Interpretation of this is that
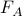is some sort of ‘effective’ version of the energy that can describe all of the states in group A! Specifically, if you want to calculate the Boltzmann weight of group A, you use 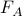as the ‘energy’. This is called the free energy.
Interpretation – a “mode” can be highly populated for either of two reasons, low energy or high entropy. Since
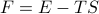.Note the temperature dependence of this! Consistent with earlier proposition that low T concentrates prob mass on the lower E ones.
Physical example: solids liquids gasses
ML example: adjusted temperature sampling in Ingraham paper to disfavor “empty” regions of space and enhance from modes
ML example: sequence generation when sampling from multinomials (the rapgen high factor)