Session 4: Diffusion part 1, random walks

be able to explain characteristics of Gaussian random walk processes without drift, with constant drift, and with origin-directed drift.
Preview: again the single molecule force spectroscopy measurement again; this time rather than binning into open/closed, consider the whole continuous reaction coordinate x.
Simplest case of diffusion with no “potential” – e.g. observation of pollen grains under a microscope, or of microbeads…
Problem setup: consider the position of a particle,
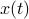 , over multiple discrete timesteps.
, over multiple discrete timesteps.present simple case of
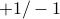 random walk; long times is Gaussian
random walk; long times is Gaussianthen generalize to
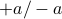 , time interval
, time interval 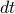 ,
, 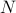 steps with
steps with 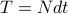 . Notation is
. Notation is 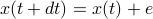 where
where 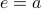 or
or 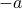 .
.generalize to other step size distributions, note the universality.
Draw some example trajectories and histograms. Note that can think of two ways, as stochastic trajectory
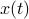 , or as a probability distribution evolving over time,
, or as a probability distribution evolving over time, 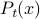 .
.Derive
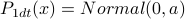 ;
; 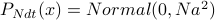 .
.generalize to higher dimensions.
Now add a constant drift term:
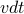 , so that each time step you move as
, so that each time step you move as 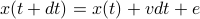 . Then
. Then 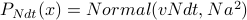 . Plot this, draw some example trajectories.
. Plot this, draw some example trajectories.How to keep the variance from exploding? Add a drift term that brings you back to the origin. Call it
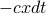 . This is like a spring, or optical trap, or what not. Then
. This is like a spring, or optical trap, or what not. Then 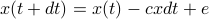 . (note this is the overdamped case where velocity = mobility
. (note this is the overdamped case where velocity = mobility 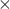 force). Next time we will derive the stationary distribution of this process
force). Next time we will derive the stationary distribution of this processFinal note: an
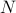 -dimensional random walk model of a polymer! Doesn't account for self-avoiding effects…
-dimensional random walk model of a polymer! Doesn't account for self-avoiding effects…