Home
Week 1
Week 2
Week 3
Week 4
Week 5
Week 6

Session 5: Diffusion part 2, differential equations

Goal

convince yourself that the Boltzmann distribution is the stationary distribution of the Fokker-Plank equation.

  • Last time: 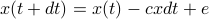x(t + dt) = x(t) - c x dt + e, or in general 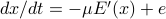dx/dt = - mu E'(x) + e. This time, derivation of partial differential equation (PDE) for p_t(x).

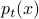  • Note that PDE's are a funky language of expressing hazy intuitive ideas into a precise mathematical picture. Like with any language, translation / understanding takes repetition. First turn ideas into equation, then manipulate equations, then interpret final result.

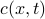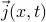  • Let's turn to diffusion from the macroscopic picture: a concentration c(x,t). Can think of as aggregate result of many individual particles, “all at once”, superimposing trajectories. And consider current vec j(x,t).

    • Fick's law: 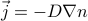vec j = - D nabla n. “which way to particles move, given some distribution?” units of particles, per unit time, per unit area.

    • And continuity equation: 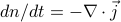dn/dt = - nabla cdot vec j. “how does concentration change due to a current?”

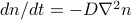    • Combining these together give the diffusion equation, dn/dt = - D nabla^2 n.

    • Interpret all of these!

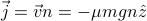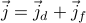  • Now let's add a bias term  —  drift term, due to an external influence. The simplest case is gravity, vec j = vec v n = -mu m g n hat z. But in general it's - mu nabla E(x) n. Then vec j = vec j_d + vec j_f  —  one from diffusion, one from force. Plugging this in we get

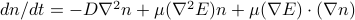    • dn/dt = -D nabla ^2 n + mu (nabla^2 E) n + mu (nabla E) cdot (nabla n).

    • means 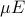mu E has same units as 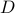D, so temperature scale is D/mu.

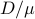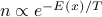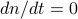  • Check that n propto e^{-E(x)/T} is a steady state solution (dn/dt = 0).

Leave a Comment Below!

Comment Box is loading comments...