Home
Introduction
Introduction
Fourier Series
Periodicity
Monsieur Fourier
Finding Coefficients
Interpretation
Hot Rings
Orthogonality
Fourier Transforms
Motivation
Inversion & Examples
Duality & Symmetry
Scaling & Derivatives
Convolution

Orthogonality

We spent the rest of class (Mon Week 2) discussing the concept of orthogonality. Prof. Osgood presented a beautifully motivated and clean picture for why it was useful to define a notion of ‘‘orthogonality’’ for functions. I won't go through the whole background of linear algebra again here, but I'll state the main point:

Main point of class

You can think of functions as vectors in an infinite-dimensional vector space. Let us consider the set of all complex-valued, square-integrable functions defined on the interval [0,1]. If you add together two such functions, you get another one, and if you scale such a function by a number, you also get another function of the same sort. So these functions form a vector space.

It turns out that this vector space has a few other nice features. A useful norm for the vector space is

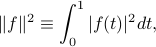
| f |^2 equiv int_0^1 | f(t) |^2 dt,

and its corresponding inner product is

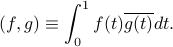
(f,g) equiv int_0^1 f(t) overline{g(t)} dt.

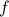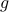We say that two functions f and g are orthogonal if (f,g) = 0.

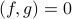We completed the analogy in class the next day (Wed Week 2), but I haven't had time to type that up yet. I'll get around to it someday.